mrasebo.blogg.se

Multiplying the Z-score by the standard deviation (shown above as 10): -2.4 x 10= -24, and.In the example above, the raw score -2.4 can be transformed back into a raw score by: Determining the raw score by adding the mean to the deviation score.Determining the deviation score by multiplying the Z-score by the standard deviation, then.Transforming a Z-score back into raw scoreĪdditionally, a Z-score can be transformed into a raw score by: The Z-score of a raw score of 26, in this given distribution, is -2.4 (negative sign means that the score is below the mean).

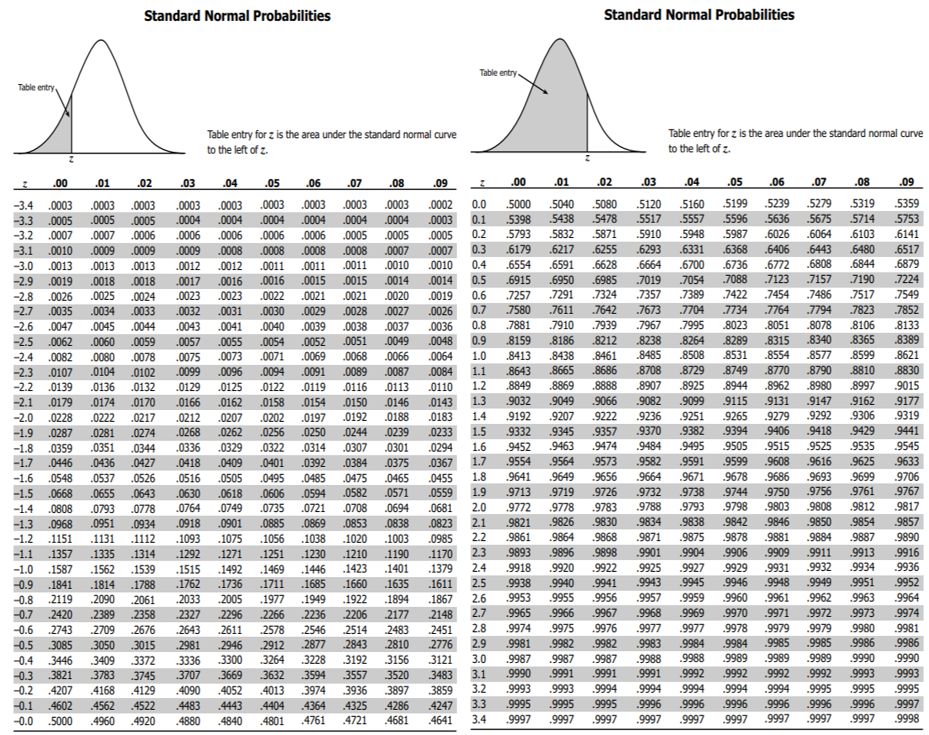
To calculate a Z-score, the mean and standard deviation are needed.įor example, if the mean of a normal distribution of class test scores is 50, and the standard deviation is 10, to calculate the Z-score for 26 the formula is applied: Where x is the standardised value- or value on the standard normal distribution, x is the value on the original distribution, µ is the mean of the original distribution, and o is the standard deviation of the original distribution. In order to be able to use this table, scores need to be converted into Z scores.Ī value from any normal distribution can be transformed into its corresponding value on a standard normal distribution using the formula: Statisticians have worked out tables for the standard normal curve that give the percentage of scores between any two points.This means that the standard normal distribution can be used to calculate the exact percentage of scores between any two points on the normal curve. Every score in a normally distributed data set has an equivalent score in the standard normal distribution.The standard normal distribution (graph below) is a mathematical-or theoretical distribution that is frequently used by researchers to assess whether the distributions of the variables they are studying approximately follow a normal curve.Each data set or distribution of scores will have their own mean, standard deviation and shape - even when they follow a normal distribution.Ī normal distribution with a mean of 0 (u=0) and a standard deviation of 1 (o= 1) is known a standard normal distribution or a Z-distribution. Normal distributions do not necessarily have the same means and standard deviations.